Shortest path: Dijkstra algorithm

An example of shortest path

The questions of this above shortest path problem example:

• What is the shortest time for traveling from the green city to the red city?
• What is the relevant shortest path?

The context of this shortest path example:

Your aim is to minimize the traveling time, which is counted with the unit of measure “hour”.

You are traveling by rail. The time is not fully linked to the distance: some trains are high-speed/mid-speed/low-speed. Between cities, there are plain/hill/mountain lands impacting the train speed.

Each city is networked to a limited number of other cities.

Take yourself some time for solving it

Finished? Ready?

The probable conclusion:

You were able to quickly find a short path, nevertheless, it was difficult to find the shortest path, due to 2 reasons:

• it’s easy to miss some paths
• it’s easy to lose track of some tracks you had already calculated

It’s why Dijkstra algorithm could be helpful

Dijkstra algorithm in very short

We will apply it in the next paragraph, right now just remember its properties:

• It’s methodical: it will, without doubt, find the shortest path
• It is applying limited shortcuts: it doesn’t calculate the paths which cannot obviously be the shortest
• It’s not hard to apply

Step-by-step application of Dijkstra on a simple example

We are simplifying the previous example for the good of the demo: the principle is exactly similar, and less time is now required.

The shortest path to solve

Imagine you want to travel from city A to city G:

Preparation of the solving tool

First, let’s create a table which will store our step-by-step process:

---

The rows of this table: at each new step we will focus on a new “milestone” city, start a new row and do some calculations

---

The columns of this table: each existing city receives 2 sub-columns:

• In the light blue background sub-cell: the distance in hours from the start city A to the city corresponding to the city owning this column
• In the light orange background sub-cell the previous city of the path, that has lead to the city owning this column

---

Step 1: starting from city A

This step is special, we fill the cell A1 in green font with:

• the distance is equal to 0, as the path from A to A is null
• the previous city is NA for “Not Applicable”: A is the starting city, hence it has no previous city
• we grey column A: we won’t come back to A, as it would mean a waste of distance, hereunder a small example why coming again to a city A would be a loss of time

Now we check which cities are linked to A: there are B, C, D

We calculate the 3 distances from A to these 3 cities:

• distance from A to B: 1 hour
• distance from A to D: 2 hours
• distance from to C: 3 hours

We fill the cells B1, C1, D1, with these distances, in red font. Remember their previous city is A

In order to choose the next city, we select the shortest path of all the table except the grey area and copy it in the next row: the winner is cell B1 with 1 hour as distance and A as previous city; it is copied in row 2, precisely in cell B2, as illustrated with the blue arrow.

Step 2: starting from city B

We grey the column B: we won’t come back to B, as it would mean a waste of distance

Now we check which cities are linked to B: the answer is E and G

We calculate the 2 distances from A to these 2 cities, trough the previous city:

• distance from A to E through B: 1+4 = 5 hours
• distance from A to G through B: 1+6 = 7 hours

We fill the cells E2, G2 with these distances, in red font. Remember their previous city is B

In order to choose the next city, we select the shortest distance of all the table, except the grey area and copy it in the next row: here cell D1, underlined, with a distance of 2 hours, and A as previous city is copied in row 3, in cell D3, as illustrated with the blue arrow

Step 3: starting from city D

We grey the column D: we won’t come back to D, as it would mean waste of distance

Now we check which cities are linked to D: the answer is no city

Hence we have no distance to calculate

We have no additional cell to fill in row 3

In order to choose the next city, we select the shortest distance of all the table except the grey area and copy it in the next row: here cell C1 with a distance of 3 hours, underlined, and A as previous city is copied in row 4, as illustrated with the blue arrow

Step 4: starting from city C

We grey the column C: we won’t come back to C, as it would mean a waste of distance

Now we check which cities are linked to C: there are F and G

We calculate the 2 distances for these 2 tracks from A to these cities, trough the previous city :

• distance from A to F through C: 3+1 = 4 hours
• distance from A to G through C: 3+6 = 9 hours

We fill the cells F4, G4 with these distances in red font. Remember their previous city is C

In order to choose the next city, we select the shortest distance of all the table except the grey area and copy it in the next row: here cell F1, underlined, with 4 as distance, and C as the previous city is copied in row 5, in cell F5, as illustrated by the blue arrow

Step 5: starting from city F

We grey the column F: we won’t come back to F, as it would mean a waste of distance

Now we check which cities are linked to F: there is G

We calculate the distance for this track from A to G, trough the previous city :

• distance from A to G: 3+1+3 = 7 hours

We fill the cell G5 with this distance in red font. Remember the previous city is F

In order to choose the next city, we select the shortest distance of all the table except the grey area and copy it in the next row: here cell E2, underlined, with a distance of 5 hours, and B as the previous city is copied in row 6, in cell E6 as described with the blue arrow

Step 6: starting from city E

We grey the column E: we won’t come back to E, as it would mean waste of distance

Now we check which cities are linked to E: there is G

We calculate the distance for this 2 tracks from A to G, trough the previous city :

• distance from A to G through E: 1+4+3 = 8 hours

We fill the cells G6 with this distance in red font. Remember their previous city is E.

In order to choose the next city, we select the shortest distance of all the table except the grey area and copy it in the next row: wait! all the table is grey. We can stop and take stock of the situation in the next step.

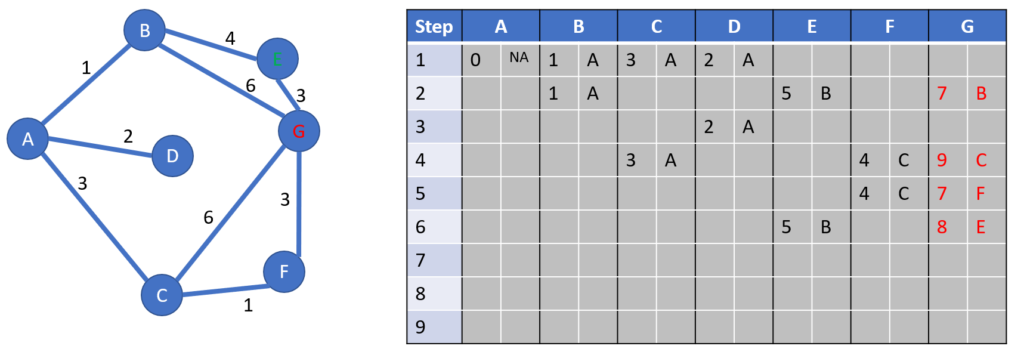
Last step : finding the winner

We focus on the target column, that is the column 6

We look for the smallest distance

There are 2 winners, with a distance of 7 hours: the path starting from B and the one starting from F

Let’s unravel the 2 paths:

• With light blue arrows: from G, the previous city is B, and its own previous city is A
• With light orange arrows: from G, the previous city is F, and its own previous city is C, and its own previous city is A

Conclusion

The shortest distance is 7

The 2 shortest paths are A -> B -> G and A -> C -> F -> G.

---

Algorithm description

We have started with a concrete example, we are ready to become more abstract: let’s describe the algorithm, as it could become the specification of a program, whatever the language

We start with the definition of the variants. There are three kinds of tables:

• unvisited cities: the cities which we have not yet studied the paths with this city, current, visited)
• current city: the milestone city from which we are investigating the nieghbor paths
• visited cities: the cities which we have already calculated the paths

The columns will be explained just after this step

Creation of variables

First we need a variable table in order to store the unvisited cities :

City

…

…

…

Then a second variable table in order to store the current city:

City	Distance from starting city	Previous City
…	…	…
…	…	…
…	…	…

Then a third variable table in order to store the visited cities

City	Distance from starting city	Previous City
…	…	…
…	…	…
…	…	…

The algorithm

1. List all cities, and store them in the unvisited table, column City
2. Is it the first time in this step?
   • If yes, select city “starting city”
   • If no, select the city from the visited table with the smallest distance AND with its corresponding City which is not in the unvisited table.
3. The city from step 2 is removed from the unvisited table
4. Look for all neighbor cities of the city from step 2. Create a row in the current table for each of these neighbors. Is it the first time in this step?
   • If yes:
     • City is “starting city”
     • Distance is “0”
     • Previous city is “NA”
   • If no :
     • City is “the considered neighbor”
     • Distance is distance from “starting city” to “city selected in step 2” (keep it mind it has already been calculated and stored in visited table) + distance from “city selected in step 2” to “the considered neighbor”
     • Previous city is “city selected in step 2”
5. Move the row(s) from the current table to the visited table
6. Is the unvisited table empty?
   • If yes: go to step 7
   • If no: repeat steps 2 to 6
7. Find in the visited table the row with City column equal to the destination city, and with the smallest Distance value. Get the previous city. Go to the row where the City column is equal to the previous city, and with the smallest Distance value. Repeat as many times as needed in order to reach the starting city as the previous city. Sum all successive distances.

---

An application with Python

Let’s use Python and the library scipy for solving this problem

We import the Dijkstra function from package scipy:

from scipy.sparse.csgraph import dijkstra

csr_matrix is required from this Dijkstra function:

from scipy.sparse import csr_matrix

We build the distances between 2 cities, for each possible coupe of cities, as a matrix. The shape of the matrix is:

	A	B	C	D	E	F	G
A
B
C
D
E
F
G

The distance between a city and itself is null, so the diagonal is filled with zeros:

	A	B	C	D	E	F	G
A	0
B		0
C			0
D				0
E					0
F						0
G							0

The distance between city X and city Y, and the one between city Y and city X, are the same. In this use case the distances are symmetrical. Hence, the package doesn’t need to repeat the information, and we fill with zeros the part under the diagonal:

	A	B	C	D	E	F	G
A	0
B	0	0
C	0	0	0
D	0	0	0	0
E	0	0	0	0	0
F	0	0	0	0	0	0
G	0	0	0	0	0	0	0

Let’s fill the first row, for city A: A has a distance of 1 with B, 3 with C, 2 with D and is not directly linked to E, F and G (when no link we set the value to 0):

	A	B	C	D	E	F	G
A	0	1	3	2	0	0	0
B	0	0
C	0	0	0
D	0	0	0	0
E	0	0	0	0	0
F	0	0	0	0	0	0
G	0	0	0	0	0	0	0

The job is completed for all other cities:

	A	B	C	D	E	F	G
A	0	1	3	2	0	0	0
B	0	0	0	0	4	0	6
C	0	0	0	0	0	1	6
D	0	0	0	0	0	0	0
E	0	0	0	0	0	0	3
F	0	0	0	0	0	0	3
G	0	0	0	0	0	0	0

The scipy algorithm doesn’t need the cities, it implies the following mapping:

• City A is index 0, equivalent to node 0
• City B is index 1, equivalent to node 1
• City C is index 2, equivalent to node 2
• …

Hence, the legend, precisely the first row and the first column can be removed:

0	1	3	2	0	0	0
0	0	0	0	4	0	6
0	0	0	0	0	1	6
0	0	0	0	0	0	0
0	0	0	0	0	0	3
0	0	0	0	0	0	3
0	0	0	0	0	0	0

Finally, Python receives this input:

graph = [
... [0,1,3,2,0,0,0],
... [0,0,0,0,4,0,6],
... [0,0,0,0,0,1,6],
... [0,0,0,0,0,0,0],
... [0,0,0,0,0,0,3],
... [0,0,0,0,0,0,3],
... [0,0,0,0,0,0,0]
... ]

Dijkstra has been programmed in order to receive csr_matrix format, so a conversion is required:

graph = csr_matrix(graph)

Indeed csr_matrix is interesting, the print function can “cast” it, meaning displaying the information in a vertical way:

print(graph)

  (0, 1)	1
  (0, 2)	3
  (0, 3)	2
  (1, 4)	4
  (1, 6)	6
  (2, 5)	1
  (2, 6)	6
  (4, 6)	3
  (5, 6)	3

Read the first line (0, 1) 1 as: the distance between the city A (because it is node 0) and the city B (because it is node 1) has a length of 1. If two cities are not linked, no row is displayed

The dijkstra function/algorithm is run:

distances_matrix, predecessors = dijkstra(csgraph=graph,                                     directed=False,                                   min_only=False,                                  indices=0,                                  return_predecessors=True)

Hereunder distance array is the list of elements of the minimum distances:

• From A to A
• From A to B
• From A to C
• …

array([0., 1., 3., 2., 5., 4., 7.])

From the above array:

• From A to A: distance is 0
• From A to B: distance is 1
• From A to C: distance is 3

The last element of the array [0., 1., 3., 2., 5., 4., 7.]provides us our main answer:

From A to G: distance is 7

Now we ask the predecessors:

predecessors

The result is again a list of elements:

array([-9999,     0,     0,     0,     1,     2,     1])

It must be understoood as:

• Index 0 (the first element): Predecessor of A
• Index 1 (the second element): Predecessor of B
• Index 2 (the third element): Predecessor of C
• …
• Index 6 (the last en element try): Predecessor of G

Remember in Python, the first element is 0, the second is 1 and so on.

In full words:

City index	City name	Predecessor node	Predecessor city
0	A	None, described by -9999	None, described by -9999
1	B	0	A
2	C	0	A
3	D	0	A
4	E	1	B
5	F	2	C
6	G	1	B

As we focus on the path to city G, we iterate the predecessor starting from it:

From G, at offset 6, the predecessor is offset 1, meaning predecessor is city B:

array([-9999,     0,     0,     0,     1,     2,     1])

From B, at offset 1, the predecessor is offset 0, meaning predecessor is city A:

array([-9999,     0,     0,     0,     1,     2,     1])

From A, at offset 0, the predecessor is offset -9999, meaning there is no predecessor:

In summary, the python program has found G is coming from B which is coming from A.
Reverting the sense, A -> B -> G

Please note this python package has provided “only” one best solution.

---

Dijkstra glossary

If you read some litterature, or discuss with some specialist, this translation table can be useful:

Our example term	Generic term
City	Node
Map	Graph
Distance	Weight

Specificity of the Dijkstra algorithm

The complexity of the problem

The algorithm provides the shortest path: it usually is an advantage.

If there are too many nodes (or cities), it induces many calculations and this could become a problem:

https://commons.wikimedia.org/wiki/File:DijkstraDemo.gif – Shiyu Ji

The complexity in the worst scenario of Dijkstra algorithm is O(|N|²) with N the number of nodes in our scenario. It means the required time increases roughly with the square of cities.

A graphical illustration, indeed displaying the function f(x) = x² and changing the labels:

Complelexity of optimized Dijkstra algorithm

Many Dijkstra libraries are optimized, like scipy which is using the Fibonacci heap.

We need to keep the overview and don’t enter in complex details: as a summary, the Fibonacci heap manages to create a priority in the order of calculation: https://en.wikipedia.org/wiki/Fibonacci_heap

And the complexity of Dijkstra algorithm optimized with Fibonacci heap becomes:

O(|E|+|N.log(|N|)) where E the number of edges and N the number of nodes

A graphical illustration, indeed displaying the function f(x) = x*log(x) and changing the labels:

What if too many nodes (cities)?

If there are too many nodes, the hereunder 2 graphs show that programming time will drastically increase.

You may not have enough calculation power available, or this calculation power doesn’t even exist yet. Thus, you’ll need other algorithms that provide a short path instead of the shortest path. We’ll investigate a scenario “too many solutions to calculate them all ” in a couple of future articles dealing with the Travel Salesman Problem (TSP)

Next article

We will study the A*algorithm (pronounce: A star) with the same small example: the basis of algorithm is same as Dijkstra, plus it adds some intelligence in order to try to guess quickly the shortest path…